Welcome to lydxlx's Blog!
-
Center of the circle passing through two points with fixed radius
The Question
Given two different points \(P = (x_1, x_2)\) and \(Q = (y_1, y_2)\) and a real number $r$, we want to compute the center of circle that pass through both points with radius $r$. It is easy to verify that there is/are (i) no solution if $r < \overline{PQ}$, (ii) exactly one solution if $r = \overline{PQ}$, and (iii) two solutions if $r > \overline{PQ}$, where $\overline{PQ}$ denotes the $L_2$ distance from $P$ to $Q$.
Step 1
Find the direction that is perpendicular to $\overrightarrow{PQ} = (x_2 - x_1, y_2-y_1)$. A simple solution is $\overrightarrow{d} = (y_1-y_2,x_2-x_1)$, where $\overrightarrow{d}$ and $\overrightarrow{PQ}$ has the same norm. Let’s denote the norm $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$ by $p$, and thus $\overrightarrow{d} / p$ will be a unit vector. For convenience, we redefine the symbol $\overrightarrow{d}$ to represent that unit vector.
Step 2
Compute the midpoint $M$ of $P$ and $Q$, where $M = ((x_1+x_2)/2, (y_1+y_2)/2)$. Now, we just need to start from $M$ and move along the direction or the opposite direction of $\overrightarrow{d}$ by $\lambda$, where $\lambda = \sqrt{r^2 - (p/2)^2}$. That is, the circle center $C$ is equal to
\[C = M \pm \lambda\overrightarrow{d}.\]Python Code
def centers(x1, y1, x2, y2, r): q = ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5 x3 = (x1 + x2) / 2 y3 = (y1 + y2) / 2 xx = (r ** 2 - (q / 2) ** 2) ** 0.5 * (y1 - y2) / q yy = (r ** 2 - (q / 2) ** 2) ** 0.5 * (x2 - x1) / q return ((x3 + xx, y3 + yy), (x3 - xx, y3 - yy))
-
合并多个Citi ThankYou Member账户
经过多次的尝试与失败,我终于搞清楚了打电话合并多个Citi ThankYou Member账户的方法,现总结如下,希望可以对您有所帮助。
-
Start on a line at correct indentation in Vim
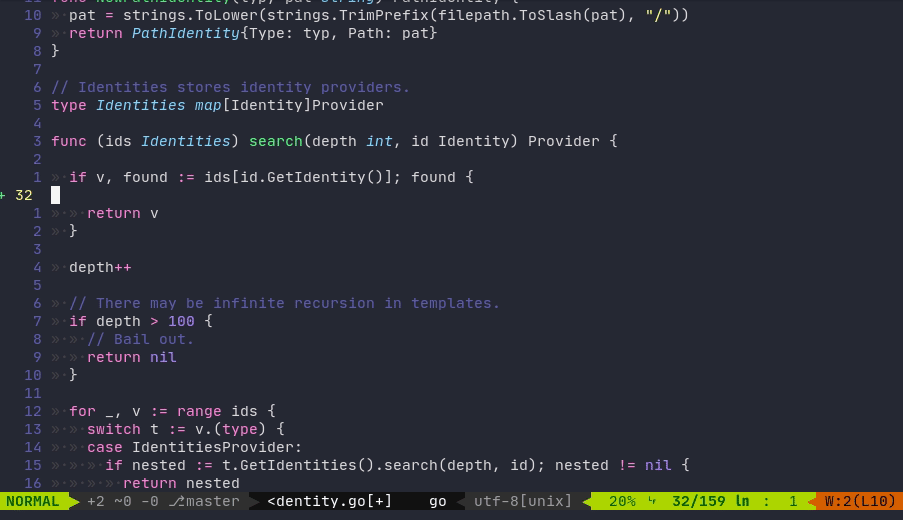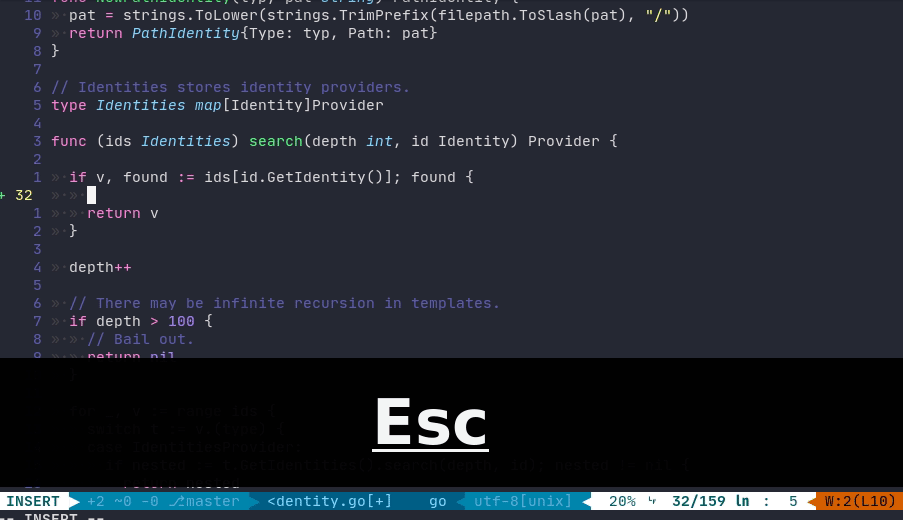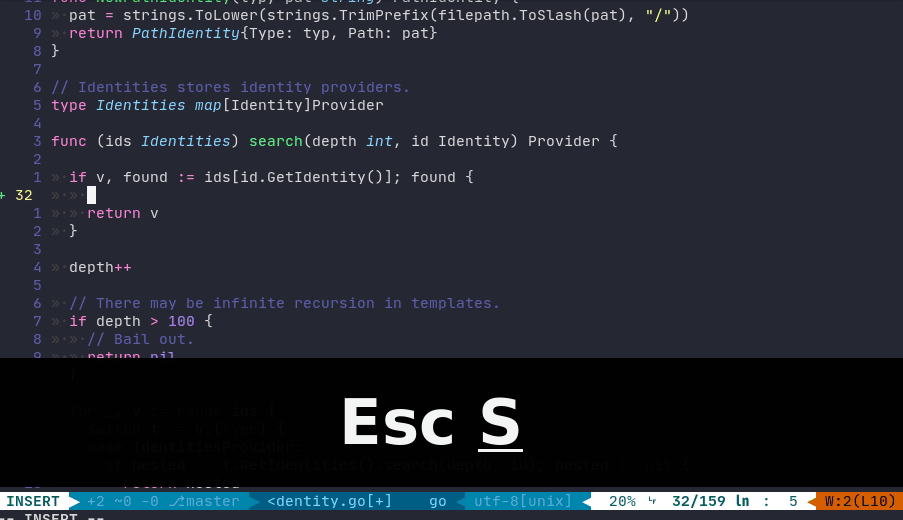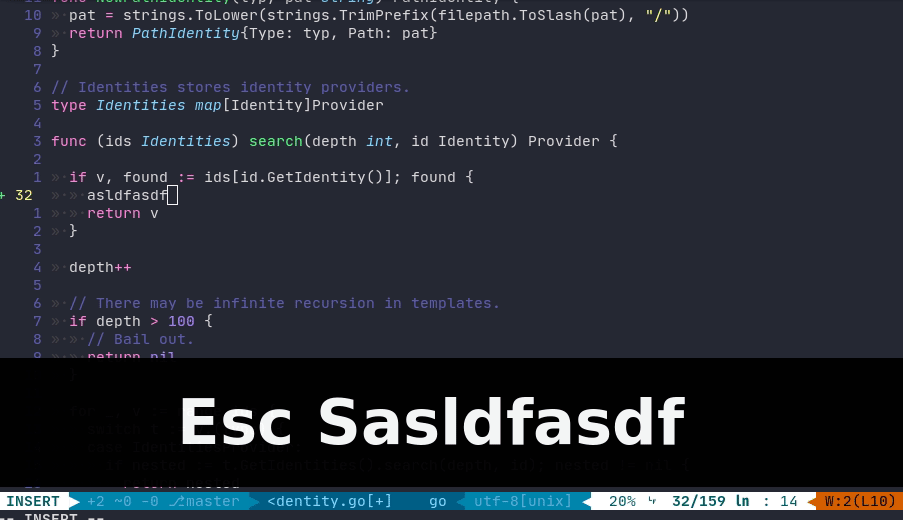
RECIPE:
S(i.e.,SHIFT+s)This will delete the current line and start to insert at the right indentation, which can be used to save some TAB typings in certain scenarios. Note that,
Sis also the synonym forcc.DEMO cited from this article:
-
Baby Wellness Guide at 7-14 Days Old
Helpful tips for this state of life.
Family Well-being
- Caregiver feelings of highs and lows are normal. If these “baby blues” are overwhelming or last for more than a few days, please talk with someone you trust (including your doctor).
- Find the support you need to help take care of yourself and your baby.
- Speak up when you down. You can call WA State Postpartum Support at 1-888-404-7763.
Nutrition
- Use breast milk or formula only.
- Give Vitamin D (400 IU/day) to babies receiving breast milk.
- Trust your instinct when feeding your baby. Hunger cues may include opening and closing the mouth, sucking on hands, smacking lips, turning the head toward your breast, acting fussy or looking unhappy. Signs of being full may include turning the head away, closing the mouth, losing interest, or falling asleep.
- Breast fed babies can learn to take a bottle at this age.
- Spitting up is common. Keeping your baby upright after feeds can help. Ask your doctor if you have concerns about associated pain, choking, or feeding problems.
- Do not give your baby extra water.
Development
- Babies prefer human stimuli (a face, voice, touch, smell) over anything else.
- Watch for your baby’s cues, including turning away or crying when she needs a break.
- Babies feel deep emotions, but lack the skills to regulate the intensity or duration of those emotions. Provide responsive and nurturing care to help your baby feel secure. This is not “spoiling” your baby.
- Tummy time and gentle activities that allow your baby to “track” objects/people can help strengthen neck muscles. Gentle massage can be introduced to share a quiet, calming time with your baby.
Newborn Care
- For babies 3 months or younger, a fever can be serious. Call us if your baby has a temperature of 100.4°F/38.0°C or higher.
- It is safe to take your baby outdoors if they are dressed appropriately and protected from the weather. Be cautious about exposing your baby to crowds or to people who may be sick.
- Caregivers can further protect their baby by updating their own vaccinations, especially the TDAP (whooping cough vaccine), MMR, and seasonal flu vaccine.
- Saline drops can be used for nasal congestion, which is common in newborns.
Safety
- Put your baby to sleep on their back. Sleep positioners are not safe for babies.
- Install the car seat in the backseat, rear-facing.
- Check to make sure smoke and carbon monoxide detectors are working.
- Avoid smoke/tobacco/cigarette/vaping liquid or smoke/marijuana exposure.
- Avoid hot liquids around your baby and set your water temperature to < 120°F (48.9°C) to prevent accidental burns.
- Provide constant supervision when your baby is around pets or siblings.
- Never shake your baby. When you are feeling overwhelmed, take a break and ask for help.
Crying
- Crying is normal way babies communicate hunger, discomfort, distress, or a need to connect with you.
- When we respond to babies quickly and sensitively, over time, they tend to cry less. They learn that care is coming.
- As your baby becomes more alert, they will begin to cry more. This is normal. Some babies cry much more than others and sometimes it can feel as if nothing works. Just by being with your baby, they learn that they can trust and rely on you. Trust yourself and reach out when you need support.
Overseas Travel
If you will be traveling with you family overseas, talk with your doctor about travel questions, or you can request an online pre-travel health consultation through out eTravel Clinic.
Credit of this post belongs to Allegro Pediatrics.
-
Numpy argmax does not populate from generator objects correctly
Consider the following examples:
import numpy as np print(np.argmax([1, 2, 3, 4])) print(np.argmax(np.array([1, 2, 3, 4]))) print("---") print(np.argmax(range(4))) print(np.argmax(np.array(range(4)))) print("---") print(np.argmax(i for i in range(4))) print(np.argmax(np.array(i for i in range(4))))The output is
3 3 --- 3 3 --- 0 0So it seems like for
np.argmax- regular list and its wrapped np array work,
- range and its wrapped np array work,
- generator object or its wrapped np array do not work.
-
Equation of the circle passing through three points
It is well known that any three non-collinear points (A, B, C) determine a unique circle passing through them. Mathematically, we can find the circle center by computing the intersection point of the perpendicular bisectors of segments AB and AC. (Pairs AB and BC or pairs AC and BC would also work.) In code implementation, however, this method can be error-prone and require extra handling when the segment slope is nearly vertical.
By searching the Internet carefully, I was finally able to find an algorithm that doesn’t deal with any slope computation, which is perfect for competitive programming. Please refer to this link for the original post. In case the website goes down in the future, I cited its content in below. The copyright all belongs to ambrsoft.
The equation of an arbitrary circle can be described by the following equation:
\[Ax^2 + Ay^2 + Bx + Cy + D = 0\]After substituting the three given points, \((x_1, y_1), (x_2, y_2)\) and \((x_3, y_3)\), which lie on the circle we get the set of equations that can be described by the determinant:
\[\begin{vmatrix} x^2 + y^2 & x & y & 1 \\ {x_1}^2 + {y_1}^2 & {x_1} & {y_1} & 1 \\ {x_2}^2 + {y_2}^2 & {x_2} & {y_2} & 1 \\ {x_3}^2 + {y_3}^2 & {x_3} & {y_3} & 1 \\ \end{vmatrix} = 0\]The coefficients \(A, B, C\) and \(D\) can be found by solving the following determinants:
\[A = \begin{vmatrix} {x_1} & {y_1} & 1\\ {x_2} & {y_2} & 1\\ {x_3} & {y_3} & 1\\ \end{vmatrix}, B = -\begin{vmatrix} {x_1}^2+{y_1}^2 & {y_1} & 1\\ {x_2}^2+{y_2}^2 & {y_2} & 1\\ {x_3}^2+{y_3}^2 & {y_3} & 1\\ \end{vmatrix}, C = \begin{vmatrix} {x_1}^2+{y_1}^2 & {x_1} & 1\\ {x_2}^2+{y_2}^2 & {x_2} & 1\\ {x_3}^2+{y_3}^2 & {x_3} & 1\\ \end{vmatrix}, D = -\begin{vmatrix} {x_1}^2+{y_1}^2 & {x_1} & {y_1}\\ {x_2}^2+{y_2}^2 & {x_2} & {y_2}\\ {x_3}^2+{y_3}^2 & {x_3} & {y_3}\\ \end{vmatrix}\]The values of \(A, B, C\) and \(D\) will be after solving the determinants: \(A = {x_1}({y_2}-{y_3}) - {y_1}({x_2}-{x_3}) + {x_2}{y_3} - {x_3}{y_2}\\ B = ({x_1}^2+{y_1}^2)({y_3}-{y_2}) + ({x_2}^2+{y_2}^2)({y_1}-{y_3}) + ({x_3}^2+{y_3}^3)({y_2}-{y_1})\\ C = ({x_1}^2+{y_1}^2)({x_2}-{x_3}) + ({x_2}^2+{y_2}^2)({x_3}-{x_1}) + ({x_3}^2+{y_3}^2)({x_1}-{x_2})\\ D = ({x_1}^2+{y_1}^2)({x_3}{y_2}-{x_2}{y_3}) + ({x_2}^2+{y_2}^2)({x_1}{y_3}-{x_3}{y_1}) + ({x_3}^2+{y_3}^2)({x_2}{y_1} - {x_1}{y_2})\)
Center point \((x, y)\) and the radius \(r\) of the circle passing through \(({x_1}, {y_1}), ({x_2}, {y_2})\) and \(({x_3}, {y_3})\) are:
\[x = -\frac{B}{2A} \\ y = -\frac{C}{2A}\\ r = \sqrt{\frac{B^2+C^2-4AD}{4A^2}}\]Here is the python code to find the circle center given three points (in format of pairs).
def center(A, B, C): (x1, y1), (x2, y2), (x3, y3) = A, B, C A = x1 * (y2 - y3) - y1 * (x2 - x3) + x2 * y3 - x3 * y2 B = (x1 ** 2 + y1 ** 2) * (y3 - y2) + (x2 ** 2 + y2 ** 2) * (y1 - y3) + (x3 ** 2 + y3 ** 2) * (y2 - y1) C = (x1 ** 2 + y1 ** 2) * (x2 - x3) + (x2 ** 2 + y2 ** 2) * (x3 - x1) + (x3 ** 2 + y3 ** 2) * (x1 - x2) return (-B / A / 2, -C / A / 2)
- 2024-01-05 美国入关记
- ChatGPT helps write an email for garbage bin replacement
- How to merge and extract tgz files from Google Takeout?
- How to auto-reload all the modules and classes in Python Notebook?
- How to hide WPM box in Typeracer?
- How to Skip Duplicate Files on Mac
- Xfinity Internet does NOT come with UNLIMITED data for free
- Union in SQL
- Baby Wellness Guide at 9 Months Old
- Baby Wellness Guide at 2 Months Old
